Logika Fuzzy

Diposting oleh Unknown Label: Catatan Kuliahku di 21:38

Pengertian Logika Fuzzy

Konsep tentang logika fuzzy diperkenalkan oleh Prof. Lotfi Astor Zadeh pada 1962. Logika fuzzy adalah metodologi sistem kontrol yang pemecah masalah, yang cocok untuk diimplementasikan pada sistem, mulai dari sistem yang sederhana, sistem kecil, embedded system, jaringan PC, multi-channel atau workstation berbasis akuisisi data, dan sistem kontrol. Logika fuzzy menurut (Kusumadewi, S & Purnomo 2004)[6] adalah sutau cara yang tepat untuk memetakan suatu ruang input ke dalam suatu ruang output. Sebagai contoh :

1. Manajer pergudangan mengatakan pada manajer produksi seberapa banyak persediaan barang pada akhir minggu ini, kemudian manajer produksi akan menetapkan jumlah barang yang harus diproduksi esok hari.

2. Anda mengatakan pada saya seberapa sejuk ruangan yang anda inginkan, saya akan mengatur putaran kipas yang ada pada ruangan ini.

Salah satu contoh pemetaan suatu input-output dalam bentuk grafis seperti terlihat pada Gambar 2.1

Gambar Contoh pemetaan input-output.

Alasan Digunakannya Logika Fuzzy

Menurut Sri Kusumadewi (2003:154)[7] beberapa alasan mengapa orang menggunakan logika fuzzy, antara lain :

1. Konsep logika fuzzy mudah dimengerti. Konsep matematis yang mendasari penalaran fuzzy sangat sederhana dan mudah dimengerti.

2. Logika fuzzy sangat fleksibel.

3. Logika fuzzy memiliki toleransi terhadap data-data yang tidak tepat.

4. Logika fuzzy mampu memodelkan fungsi-fungsi nonlinear yang sangat kompleks.

5. Logika fuzzy dapat membangun dan mengaplikasikan pengalaman- pengalaman para pakar secara langsung tanpa harus melalui proses pelatihan.

6. Logika fuzzy dapat bekerjasama dengan teknik-teknik kendali secara konvensional.

7. Logika fuzzy didasarkan pada bahasa alami.

Aplikasi Logika Fuzzy

Beberapa aplikasi logika fuzzy, antara lain (Kusumadewi, Sri, 2003:155)[7] :

1. Pada tahun 1990 pertama kali dibuat mesin cuci dengan logika fuzzy di Jepang (Matsushita Electric Industrial Company). Sistem fuzzy digunakan untuk menentukan putaran yang tepat secara otomatis berdasarkan jenis dan banyaknya kotoran serta jumlah yang akan dicuci. Input yang digunakan adalah : seberapa kotor, jenis kotoran, dan banyaknya yang dicuci. Mesin ini menggunakan sensor optik, mengeluarkan cahaya ke air dan mengukur bagaimana cahaya tersebut sampai ke ujung lainnya. Makin kotor, maka sinar yang sampai makin redup. Disamping itu, sistem juga dapat menentukan jenis kotoran (daki atau minyak).

2. Transmisi otomatis pada mobil. Mobil Nissan telah menggunakan sistem fuzzy pada transmisi otomatis, dan mampu menghemat bensin 12 – 17%.

3. Kereta bawah tanah Sendai mengontrol pemberhentian otomatis pada area tertentu.

4. Ilmu kedokteran dan biologi, seperti sistem diagnosis yang didasarkan pada logika fuzzy, penelitian kanker, manipulasi peralatan prostetik yang didasarkan pada logika fuzzy, dll.

5. Manajemen dan pengambilan keputusan, seperti manajemen basisdata yang didasarkan pada logika fuzzy, tata letak pabrik yang didasarkan pada logika fuzzy, sistem pembuat keputusan di militer yang didasarkan pada logika fuzzy, pembuatan games yang didasarkan pada logika fuzzy, dll.

6. Ekonomi, seperti pemodelan fuzzy pada sistem pemasaran yang kompleks, dll.

7. Klasifikasi dan pencocokan pola.

8. Psikologi, seperti logika fuzzy untuk menganalisis kelakuan masyarakat, pencegahan dan investigasi kriminal, dll.

9. Ilmu-ilmu sosial, terutam untuk pemodelan informasi yang tidak pasti.

10. Ilmu lingkungan, seperti kendali kualitas air, prediksi cuaca, dll.

11. Teknik, seperti perancangan jaringan komputer, prediksi adanya gempa bumi, dll.

12. Riset operasi, seperti penjadwalan dan pemodelan, pengalokasian, dll.

13. Peningkatan kepercayaan, seperti kegagalan diagnosis, inspeksi dan monitoring produksi.

Dasar-dasar Logika Fuzzy

Untuk memahami logika fuzzy, sebelumnya perhatikan dahulu tentang konsep himpunan fuzzy. Himpunan fuzzy memiliki 2 atribut, (Sutojo et al, 2011:212)[8] yaitu :

1. Linguistik, yaitu nama suatu kelompok yang mewakili suatu keadaan tertentu dengan menggunakan bahasa alami, misalnya : DINGIN, SEJUK, PANAS mewakili variabel temperatur. Contoh lain misalnya MUDA, PAROBAYA, TUA mewakili variabel umur.

2. Numeris, yaitu suatu nilai yang menunjukkan ukuran dari suatu variabel misalnya : 10, 35, 40, dan sebagainya.

Disamping itu ada beberapa hal yang perlu diketahui dalam memahami sistem fuzzy, (Sutojo et al, 2011:212)[8] yaitu :

1. Variabel fuzzy

Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu sistem fuzzy. Contoh : umur, temperatur, permintaan, dsb.

2. Himpunan fuzzy

Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variabel fuzzy.

Contoh :

· Variabel umur, terbagi menjadi 3 himpunan fuzzy, yaitu: MUDA, PAROBAYA, dan TUA. (Gambar 2.2)

Gambar 2.2 Himpunan fuzzy untuk variabel Umur.

· Variabel temperatur, terbagi menjadi 5 himpunan fuzzy, yaitu : DINGIN, SEJUK, NORMAL, HANGAT, dan PANAS. (Gambar 2.3)

Gambar 2.3 Himpunan fuzzy pada variabel temperatur.

3. Semesta Pembicaraan

Menurut Sri Kusumadewi (2003:159)[7], Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif maupun negatif. Adakalanya nilai semesta pembicaraan ini tidak dibatasi batas atasnya.

Contoh :

· Semesta pembicaraan untuk variabel umur: [0 +∞)

· Semesta pembicaraan untuk variabel temperatur: [0 40]

4. Domain

Menurut Sri Kusumadewi (2003:159)[7], Domain himpunan fuzzy adalah keseluruhan nilai yang diijinkan dalam semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy. Seperti halnya semesta pembicaraan, domain merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai domain dapat berupa bilangan positif maupun negatif.

Contoh domain himpunan fuzzy :

· MUDA = [0 45]

· PABOBAYA = [35 55]

· TUA = [45 +∞)

· DINGIN = [0 20]

· SEJUK = [15 25]

· NORMAL = [20 30]

· HANGAT = [25 35]

· PANAS = [30 40]

Fungsi Keanggotaan

Fungsi Keanggotaan (membership function) adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotaannya (sering juga disebut dengan derajat keanggotaan) yang memiliki interval antara 0 sampai 1. Salah satu cara yang dapat digunakan untuk mendapatkan nilai keanggotaan adalah dengan melalui pendekatan fungsi. Ada beberapa fungsi yang bisa digunakan (Kusumadewi, Sri, 2003)[7] :

a. Representasi Linear

Pada representasi linear, pemetaan input ke derajat keanggotannya digambarkan sebagai suatu garis lurus. Bentuk ini paling sederhana dan menjadi pilihan yang baik untuk mendekati suatu konsep yang kurang jelas.

Ada 2 keadaan himpunan fuzzy yang linear. Pertama, kenaikan himpunan dimulai pada nilai domain yang memiliki derajat keanggotaan nol [0] bergerak ke kanan menuju ke nilai domain yang memiliki derajat keanggotaan lebih tinggi

(Gambar 2.4)

Gambar 2.4 Representasi Linear Naik.

Fungsi Keanggotaan :

µ[x] = (2.1)

Contoh 2.1:

Fungsi keanggotaan untuk himpunan PANAS pada variabel temperatur ruangan seperti terlihat pada Gambar 2.5.

µPANAS[32] = (32-25)/(35-25)

= 7/10 = 0,7

Gambar 2.5 Himpunan fuzzy: PANAS.

Kedua, merupakan kebalikan yang pertama. Garis lurus dimulai dari nilai domain dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak menurun ke nilai domain yang memiliki derajat keanggotaan lebih rendah (Gambar 2.6).

Gambar 2.6 Representasi Linear Turun.

Fungsi Keanggotaan :

(2.2)

Contoh 2.2:

Fungsi keanggotaan untuk himpunan DINGIN pada variabel temperatur ruangan seperti terlihat pada Gambar 2.7.

µDINGIN[20] = (30-20)/(30-15)

= 10/15 = 0,667

Gambar 2.7 Himpunan fuzzy: DINGIN.

b. Representasi Kurva Segitiga

Kurva Segitiga pada dasarnya merupakan gabungan antara 2 garis

(linear) seperti terlihat pada Gambar 2.8.

Gambar 2.8 Kurva Segitiga.

Fungsi Keanggotaan :

µ[x] = (2.3)

Contoh 2.3:

Fungsi keanggotaan untuk himpunan NORMAL pada variabel temperatur ruangan seperti terlihat pada Gambar 2.9.

µNORMAL[23] = (23-15)/(25-15)

= 8/10 = 0,8

Gambar 2.9 Himpunan fuzzy: NORMAL (kurva segitiga).

c. Representasi Kurva Trapesium

Kurva Segitiga pada dasarnya seperti bentuk segitiga, hanya saja ada beberapa titik yang memiliki nilai keanggotaan 1

(Gambar 2.10).

Gambar 2.10 Kurva Trapesium.

Fungsi Keanggotaan :

µ[x] = (2.4)

Contoh 2.6:

Fungsi keanggotaan untuk himpunan NORMAL pada variabel temperatur ruangan seperti terlihat pada Gambar 2.11.

µNORMAL[23] = (35-32)/(35-27)

= 3/8 = 0,375

Gambar 2.11 Himpunan fuzzy: NORMAL (kurva trapesium).

d. Representasi Kurva Bentuk Bahu

Daerah yang terletak di tengah-tengah suatu variabel yang direpresentasikan dalam bentuk segitiga, pada sisi kanan dan kirinya akan naik dan turun (misalkan: DINGIN bergerak ke SEJUK bergerak ke HANGAT dan bergerak ke PANAS). Tetapi terkadang salah satu sisi dari variabel tersebut tidak mengalami perubahan. Sebagai contoh, apabila telah mencapai kondisi PANAS, kenaikan temperatur akan tetap berada pada kondisi PANAS. Himpunan fuzzy ‘bahu’, bukan segitiga, digunakan untuk mengakhiri variabel suatu daerah fuzzy. Bahu kiri bergerak dari benar ke salah, demikian juga bahu kanan bergerak dari salah ke benar. Gambar 2.12 menunjukkan variabel TEMPERATUR dengan daerah bahunya.

Gambar 2.12 Daerah ‘bahu’ pada variabel TEMPERATUR.

e. Representasi Kurva-S

Kurva PERTUMBUHAN dan PENYUSUTAN merupakan kurva-S atau sigmoid yang berhubungan dengan kenaikan dan penurunan permukaan secara tak linear. Kurva-S untuk PERTUMBUHAN akan bergerak dari sisi paling kiri (nilai keanggotaan = 0) ke sisi paling kanan (nilai keanggotaan = 1). Fungsi keanggotaannya akan tertumpu pada 50% nilai keanggotaannya yang sering disebut dengan titik infleksi (Gambar 2.13).

Gambar 2.13 Himpunan fuzzy dengan kurva-S : PERTUMBUHAN.

Kurva-S untuk PENYUSUTAN akan bergerak dari sisi paling kanan (nilai keanggotaan = 1) ke sisi paling kiri (nilai keanggotaan = 0) seperti telihat pada Gambar 2.14.

Gambar 2.14 Himpunan fuzzy dengan kurva-S: PENYUSUTAN.

Kurva-S didefinisikan dengan menggunakan 3 parameter, yaitu: nilai keanggotaan nol (α), nilai keanggotaan lengkap (γ), dan titik infleksi atau crossover (β) yaitu titik yang memiliki domain 50% benar. Gambar 2.15 menunjukkan karakteristik kurva-S dalam bentuk skema.

Gambar 2.15 Karakteristik fungsi kurva-S.

Fungsi keangotaanpada kurva PERTUMBUHAN adalah :

S(x;α,β,γ) = (2.5)

Contoh 2.7:

Fungsi keanggotaan untuk himpunan TUA pada variabel umur seperti terlihat pada Gambar 2.16.

µTUA[50] = 1 – 2((60-50)/(60-35))2

= 1 – 2(10/25)2

= 0,68

Gambar 2.16 Himpunan Fuzzy: TUA.

Sedangkan fungsi keanggotaan pada kurva PENYUSUTAN adalah :

S(x;α,β,γ) = (2.6)

Contoh 2.8:

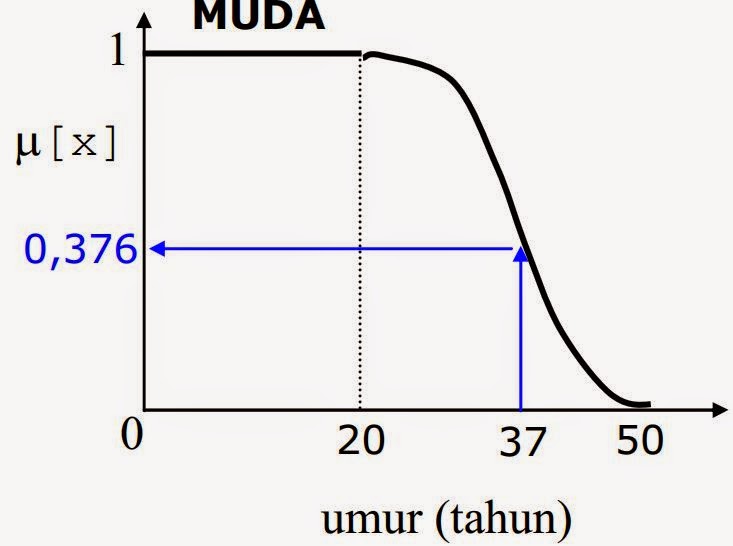
Fungsi keanggotaan untuk himpunan MUDA pada variabel umur seperti terlihat pada Gambar 2.17.

µMUDA[50] = 2((50-37)/(50-20))2

= 2(13/30)2

= 0,376

Gambar 2.17 Himpunan Fuzzy: MUDA.

f. Representasi Kurva Bentuk Lonceng (Bell Curve)

Untuk merepresentasikan bilangan fuzzy, biasanya digunakan kurva berbentuk lonceng. Kurva berbentuk lonceng ini terbagi atas 3 kelas, yaitu: himpunan fuzzy PI, beta, dan Gauss. Perbedaan ketiga kurva ini terletak pada gradiennya.

i. Kurva PI

Kurva PI berbentuk lonceng dengan derajat keanggotaan 1 terletak pada pusat dengan domain (γ), dan lebar kurva (β) seperti terlihat pada Gambar 2.18. Nilai kurva untuk suatu nilai domain x diberikan sebagai :

Gambar 2.18 Karakteristik fungsional kurva PI.

Fungsi Keanggotaan:

П(x,β,γ) = (2.7)

Contoh 2.9:

Fungsi keanggotaan untuk himpunan PAROBAYA pada variabel umur seperti terlihat pada Gambar 2.19.

µ1/2BAYA[42] = 1 - 2((45-42)/(45-35))2

= 1 - 2(3/10)2

= 0,82

µ1/2BAYA[51] = 2((55-51)/(55-45))2

= 2(4/10)2

= 0,32

Gambar 2.19 Himpunan Fuzzy: PAROBAYA dengan kurva phi.

ii. Kurva BETA

Seperti halnya kurva PI, kurva BETA juga berbentuk lonceng namun lebih rapat. Kurva ini juga didefinisikan dengan 2 parameter, yaitu nilai pada domain yang menunjukkan pusat kurva (γ), dan setengah lebar kurva (β) seperti terlihat pada Gambar 2.20. Nilai kurva untuk suatu nilai domain x diberikan sebagai :

Gambar 2.20 Karakteristik fungsional kurva BETA.

Fungsi Keanggotaan :

B(x; γ,β) = (2.8)

Salah satu perbedaan mencolok kurva BETA dari kurva PI adalah, fungsi keanggotaannya akan mendekati nol hanya jika nilai (β) sangat besar.

Contoh 2.10:

Fungsi keanggotaan untuk himpunan SETENGAH BAYA pada variabel umur seperti terlihat pada Gambar 2.21.

µ1/2BAYA[42] = 1/(1+((42-45)/5)2)

= 0,7353

µ1/2BAYA[51] = 1/(1+((51-45)/5)2)

= 0,4098

Gambar 2.21 Himpunan Fuzzy: SETENGAH BAYA dengan kurva Beta.

iii. Kurva GAUSS

Jika kurva PI dan kurva BETA menggunakan 2 parameter yaitu (γ) dan (β), kurva GAUSS juga menggunakan (γ) untuk menunjukkan nilai domain pada pusat kurva, dan (k) yang menunjukkan lebar kurva (Gambar 2.22). Nilai kurva untuk suatu nilai domain x diberikan sebagai :

Gambar 2.22 Karakteristik fungsional kurva GAUSS.

Fungsi Keanggotaan :

G(x; k, γ) = (2.9)

2.2.5 Operator dasar zadeh untuk operasi himpunan fuzzy

Seperti halnya himpunan konvensional, ada beberapa operasi yang didefinisikan secara khusus untuk mengkombinasi dan memodifikasi himpunan fuzzy. Nilai keanggotaan sebagai hasil dari operasi 2 himpunan sering dikenal dengan nama fire strength atau α–predikat. Ada 3 operator dasar yang diciptakan oleh Zadeh, yaitu :

2.2.6.1 Operator AND

Operator ini berhubungan dengan operasi interseksi pada himpunan. α– predikat sebagai hasil operasi dengan operator AND diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan- himpunan yang bersangkutan.

µ_AÇ µ_B = Min(µ_A[x], µ_B[y]) (2.10)

Contoh 2.11:

Misalkan nilai keanggotaan 27 tahun pada himpunan MUDA adalah 0,6 (µ_Muda [27]=0,6); dan nilai keanggotaan Rp 2.000.000,- pada himpunan penghasilan TINGGI adalah 0,8 (µ_{Gaji Tinggi} [2x106]=0,8); maka α–predikat untuk usia MUDA dan berpenghasilan TINGGI adalah:

µ_MudaÇ µ_{Gaji Tinggi}= Min(µ_Muda[27], µ_Gaji
Tinggi[2x10⁶]

= Min(0,6; 0,8)

= 0,6

2.2.6.2 Operator OR

Operator ini berhubungan dengan operasi union pada himpunan. a– predikat sebagai hasil operasi dengan operator OR diperoleh dengan mengambil nilai keanggotaan terbesar antar elemen pada himpunan- himpunan yang bersangkutan.

µ_AÈ µ_B = Max(µ_A[x], µ_B[y]) (2.11)

Contoh 2.12:

Pada contoh 7.11, dapat dihitung nilai a–predikat untuk usia MUDA atau berpenghasilan TINGGI adalah:

µ_MudaÈ µ_{Gaji Tinggi}= Min(µ_Muda[27], µ_Gaji
Tinggi[2x10⁶]

= Min(0,6; 0,8)

= 0,8

2.2.6.3 Operator NOT

Operator ini berhubungan dengan operasi komplemen pada himpunan. a– predikat sebagai hasil operasi dengan operator NOT diperoleh dengan mengurangkan nilai keanggotaan elemen pada himpunan yang bersangkutan dari 1.

µ_A`= 1-µ_A[x] (2.12)

Contoh 2.13:

Pada contoh 7.11, dapat dihitung nilai a–predikat untuk usia TIDAK MUDA adalah:

µ_Muda`[27]= 1-µ_Muda[27]

= 1 - 0,6

= 0,4

2.2.6 Fungsi Implikasi

Tiap-tiap aturan (proposisi) pada basis pengetahuan fuzzy akan berhubungan dengan suatu relasi fuzzy. Bentuk umum dari aturan yang digunakan dalam fungsi implikasi adalah :

IF x is A THEN y is B

dengan x dan y adalah skalar, dan A dan B adalah himpunan fuzzy. Proposisi yang mengikuti IF disebut sebagi anteseden, sedangkan proposisi yang mengikuti THEN disebut sebagai konsekuen. Proposisi ini dapat diperluas dengan menggunakan operator fuzzy, seperti :

IF (x1 is A1) • (x2 is A2) • (x3 is A3) • ...... • (xN is AN) THEN y is B

dengan • adalah operator (misal: OR atau AND).

Secara umum, ada 2 fungsi implikasi yang dapat digunakan, (Sutojo et al, 2011:230)[8] yaitu :

a. Min (minimum). Fungsi ini akan memotong output himpunan fuzzy. Gambar 2.23 menunjukkan salah satu contoh penggunaan fungsi min.

Gambar 2.23 Fungsi implikasi: MIN.

b. Dot (product). Fungsi ini akan menskala output himpunan fuzzy. Gambar 2.24 menunjukkan salah satu contoh penggunaan fungsi dot.

Gambar 2.24 Fungsi implikasi: DOT.

2.2.7 Cara Kerja Logika Fuzzy

Untuk memahami cara kerja logika fuzzy, perhatikan struktur elemen dasar sistem inferensi fuzzy berikut (Gambar 2.25) (Sutojo et al, 2011:232)[8].

Gambar 2.25 Struktur sistem inferensi fuzzy

Keterangan:

Basis Pengetahuan Fuzzy: kumpulan rule-rule fuzzy dalam bentuk pernyataan IF…THEN.

Fuzzyfikasi: proses untuk mengubah input sistem yang mempunyai nilai tegas menjadi variabel linguistik menggunakan fungsi keanggotaan yang disimpan dalam basis pengetahuan fuzzy.

Mesin inferensi: proses untuk mengubah input fuzzy menjadi output fuzzy dengan cara mengikuti aturan-aturan (IF-THEN Rule) yang telah ditetapkan pada basis pengetahuan fuzzy.

Defuzzifikasi: mengubah output fuzzy yang diperoleh dari mesin inferensi menjadi nilai tegas menggunakan fungsi keanggotaan yang sesuai dengan saat dilakukan fuzzyfikasi.

Cara kerja logika fuzzy, meliputi beberapa tahapan berikut:

1. Fuzzyfikasi

2. Pembentukan basis pengetahuan fuzzy (Rule dalam bentuk IF…THEN)

3. Mesin inferensi (Fungsi implikasi Max-Min atau Dot-Product)

4. Defuzzyfikasi

Banyak cara untuk melakukan defuzzyfikasi, di antaranya metode berikut.

a. Metode Rata-Rata (Average)

(2.13)

b. Metode Titik Tengah (Center of area)

(2.14)

2.2.8 Metode Fuzzy Inference System (FIS) Tsukamoto

Pada Metode Tsukamoto, setiap konsekuen pada aturan yang berbentuk IF-Then harus direpresentasikan dengan suatu himpunan fuzzy dengan fungsi keanggotaan yang monoton (Gambar 2.26). Sebagai hasilnya, output hasil inferensi dari tiap-tiap aturan diberikan secara tegas (crisp) berdasarkan α-predikat (fire strength). Hasil akhirnya diperoleh dengan menggunakan rata-rata terbobot. (Sri Kusumadewi, 2003:180)[7].

Gambar 2.26 Inferensi dengan menggunakan Metode Tsukamoto.

Contoh 2.14:

Suatu perusahaan makanan kaleng akan memproduksi makanan jenis ABC. Dari data 1 bulan terakhir, permintaan terbesar hingga mencapai 5000 kemasan/hari, dan permintaan terkecil sampai 1000 kemasan/hari. Persediaan barang digudang terbanyak sampai 600 kemasan/hari, dan terkecil pernah sampai 100 kemasan/hari. Dengan segala keterbatasannya, sampai saat ini, perusahaan baru mampu memproduksi barang maksimum 7000 kemasan/hari, serta demi efisiensi mesin dan SDM tiap hari diharapkan perusahaan memproduksi paling tidak 2000 kemasan. Apabila proses produksi perusahaan tersebut menggunakan 4 aturan fuzzy sbb:

[R1] IF Permintaan TURUN And Persediaan BANYAK

THEN Produksi Barang BERKURANG;

[R2] IF Permintaan TURUN And Persediaan SEDIKIT

THEN Produksi Barang BERKURANG;

[R3] IF Permintaan NAIK And Persediaan BANYAK

THEN Produksi Barang BERTAMBAH;

[R4] IF Permintaan NAIK And Persediaan SEDIKIT

THEN Produksi Barang BERTAMBAH;

Berapa kemasan makanan jenis ABC yang harus diproduksi, jika jumlah permintaan sebanyak 4000 kemasan, dan persediaan di gudang masih 300 kemasan?

Solusi:

Ada 3 variabel fuzzy yang akan dimodelkan, yaitu:

• Permintaan; terdiri-atas 2 himpunan fuzzy, yaitu: NAIK dan TURUN (Gambar 2.27).

Gambar 2.27 Fungsi keanggotaan variabel Permintaan pada Contoh 2.14.

µ_PmtTURUN[x] =

µ_PmtNaik[x] =

Kita bisa mencari nilai keanggotaan:

µPmtTURUN[4000] = (5000-4000)/4000

= 0,25

µPmtNAIK[4000] = (4000-1000)/4000

= 0,75

• Persediaan; terdiri-atas 2 himpunan fuzzy, yaitu: SEDIKIT dan BANYAK (Gambar 2.28).

Gambar 2.28 Fungsi keanggotaan variabel Persediaan pada Contoh 2.14.

µ_PsdSEDIKIT[y] =

µ_PsdBANYAK[y] =

Kita bisa mencari nilai keanggotaan :

µPsdSEDIKIT[300] = (600-300)/500

= 0,6

µPsdBANYAK[300] = (300-100)/500

= 0,4

• Produksi barang; terdiri-atas 2 himpunan fuzzy, yaitu: BERKURANG dan BERTAMBAH (Gambar 2.29).

Gambar 2.29 Fungsi keanggotaan variabel Produksi Barang pada Contoh 2.14.

µ_{PrBrgBERKURANG}[y] =

µ_{PrBrgBERTAMBAH}[y] =

Sekarang kita cari nilai z untuk setiap aturan dengan menggunakan fungsi MIN pada aplikasi fungsi implikasinya:

[R1] IF Permintaan TURUN And Persediaan BANYAK

THEN Produksi Barang BERKURANG;

α-predikat1 = µPmtTURUN ∩ PsdBANYAK

= min(µPmtTURUN [4000],µPsdBANYAK[300])

= min(0,25; 0,4)

= 0,25

Lihat himpunan Produksi Barang BERKURANG,

(7000-z)/5000 = 0,25 ---> z1 = 5750

[R2] IF Permintaan TURUN And Persediaan SEDIKIT

THEN Produksi Barang BERKURANG;

α-predikat2 = µPmtTURUN ∩ PsdSEDIKIT

= min(µPmtTURUN [4000],µPsdSEDIKIT[300])

= min(0,25; 0,6)

= 0,25

Lihat himpunan Produksi Barang BERKURANG,

(7000-z)/5000 = 0,25 ---> z2 = 5750

[R3] IF Permintaan NAIK And Persediaan BANYAK

THEN Produksi Barang BERTAMBAH;

α-predikat3 = µPmtNAIK ∩ PsdBANYAK

= min(µPmtNAIK [4000],µPsdBANYAK[300])

= min(0,75; 0,4)

= 0,4

Lihat himpunan Produksi Barang BERTAMBAH,

(z-2000)/5000 = 0,4 ---> z3 = 4000

[R4] IF Permintaan NAIK And Persediaan SEDIKIT

THEN Produksi Barang BERTAMBAH;

α-predikat4 = µPmtNAIK ∩ PsdBANYAK

= min(µPmtNAIK [4000],µPsdSEDIKIT[300])

= min(0,75; 0,6)

= 0,6

Lihat himpunan Produksi Barang BERTAMBAH,

(z-2000)/5000 = 0,6 ---> z4 = 5000

Dari sini kita dapat mencari berapakah nilai z, yaitu:

Z =

Z = = = 4983

Jadi jumlah makanan kaleng jenis ABC yang harus diproduksi sebanyak 4983 kemasan.

2.1 Mean Absolute Percentage Error (MAPE)

MAPE adalah rata-rata persentase absolut dari kesalahan peramalan dengan menghitung error absolut tiap periode. Error ini kemudian dibagi dengan n. Rumus dari MAPE ini adalah sebagai berikut :

MAPE = x 100% (2.15)

Keterangan :

Xt = Nilai data periode ke-t

Ft = Nilai ramalan periode ke-t

n = banyaknya data

Posting Komentar

Ayo berikan Komentarmu, karena satu komentar dari kamu itu sangat berarti bagi saya (^_^)